The Set Theory Guide for Artists Chapter 3: Part 3

It's time for elementary embeddings

Jun 20, 2025

Recently, an archaeological discovery of great importance has been recovered. It is a transcript of an ancient meeting between the producers of the universe. The transcript was found sealed in the ark of the measurable cardinal. It was dusted off and translated into English (from the ancient language) in the early summer of 2025. It is typed here exactly as it was translated, word for word.

PART 1: WHERE IN THE WORLD DID THE WORLD COME FROM

PART 2: HONEY, WE NEED TO TALK ABOUT WEAKLY COMPACT CARDINALS

PART 3: IT’S TIME FOR ELEMENTARY EMBEDDINGS

PART 4: THE SET FORMATION CHAPTER PAINTING

PART 3: IT’S TIME FOR ELEMENTARY EMBEDDINGS

*The Ancient of Days setting a Compass to the Earth*, frontispiece to copy K of *Europe a Prophecy* by William Blake 1794

THE PRODUCERS’ CUT

Producer 15: I think we should take an ultrapower of the universe.

Producer 29: Ultra power of the universe. Ultra power of the universe. Do you even hear the words that are coming out of you? We’ve been sitting here for what 20 hours and we have no ideas and now we are just making up words?

Producer 3: Let’s all just - maybe we need a snack. We’ve been here for a while. I think we’re all just getting a little punchy.

Producer 100: Creating a universe from the universe takes time right guys!? We’ll figure it out.

Producer ω: Löwenheim-Skolem downward anyone?

Producer ω₁: It’s been done!

Producer 29: Maybe if we I don’t know had a bigger budget, maybe something more than the universe if we are trying to make another bigger other universe?

Producer 15: I know it sounds crazy. I know it sounds completely insane. In the end we’ll probably get something crazy like a universe smaller than the universe that is actually bigger than the universe like that weird dream I had and then we’ll all know that we’ve all completely lost our minds but hear me out. I have a plan.

Producer 15: We start with the universe V and then we make many many copies of V, that is we make a κ-product of V:

$V^{\kappa} $

Does anyone have a cardinal κ we can use?

Producer 1: How big are we talking? I have a cardinal from our recent ultrafilter production. Actually you might like the show.

Producer 15: I’ve seen it! That’s perfect. Actually I forgot to mention we need a nonprincipal ultrafilter on κ.

Producer 1: Done.

Producer 15: Great! This might actually work. So we have this κ-product or rather we can call it a κ-power of the universe since it is multiple copies of the same universe.

Producer 30: That might not be a universe! A product of models of ZFC is not a model of ZFC! Any element of the product that has an empty coordinate can’t have any elements if one of its coordinates can’t have any elements so you’ve got an abundance of empty sets!

Producer 29: This is a waste of resources!

Producer 15: You’re totally right! It’s not a universe … yet. Is everyone familiar with the reincarnation illusion via equivalence classes?

Producer 0: Please remind us.

Producer 15: The reincarnation illusion is that there are souls which are in the same equivalence class or particular type of soul born at different times from each other giving the illusion of a reincarnation of souls. For example a costume designer might die on October 24, 1981 and a set-theorist born on December 23, 1981 with similarities which gives the impression of a reincarnated soul. They are not the same soul but they are in the same equivalence class of souls. We are going to form equivalence classes of our κ-power universe. In this world it is like one person is the entire collection of people in the same reincarnation illusion cohort. We are forming an ultrapower and instead of just a power to get closer the truth in V.

Producer 16: When are two elements of the κ-power in the same equivalence class?

Producer 15: When the set of coordinates where they are the same is in the ultrafilter.

Producer 17: Oh I get it. Two elements of the product are in the same equivalence class if they agree on a “big” subset of κ. Big sets are sets in the ultrafilter, small sets are sets not in the ultrafilter. Does the ultrafilter have a name?

Producer 15: Yes you got it. Let’s call the ultrafilter U. If f

$f: \kappa \to V$

and

$g: \kappa \to V$

are elements of

$V^{\kappa}$

then

$f \sim_{U} g \ \iff \{\alpha \in \kappa \ : \ f(\alpha)= g(\alpha) \} \in U. $

So the equivalence class of f is all the other elements of the product that agree with f on a big set:

$[f] = \{ g \in V^{\kappa} \ : \ f \sim_U g \}$

and finally we can say that the ultrapower of V is

$V^U = V^{\kappa} /_{\sim_U} = \{[f] \ : \ f : \kappa \to V \}$

And look we can just say for

$f, g \in V^{\kappa}$

that

$[f] \in_{U} [g]$

if and only if

$\{ \alpha < \kappa \ : \ f(\alpha) \in g(\alpha) \} \in U.$

So that our new universe is

$V^U$

with signature

$\in_U.$

See! It’s another universe!

Producer 11: How do we know it is a universe?

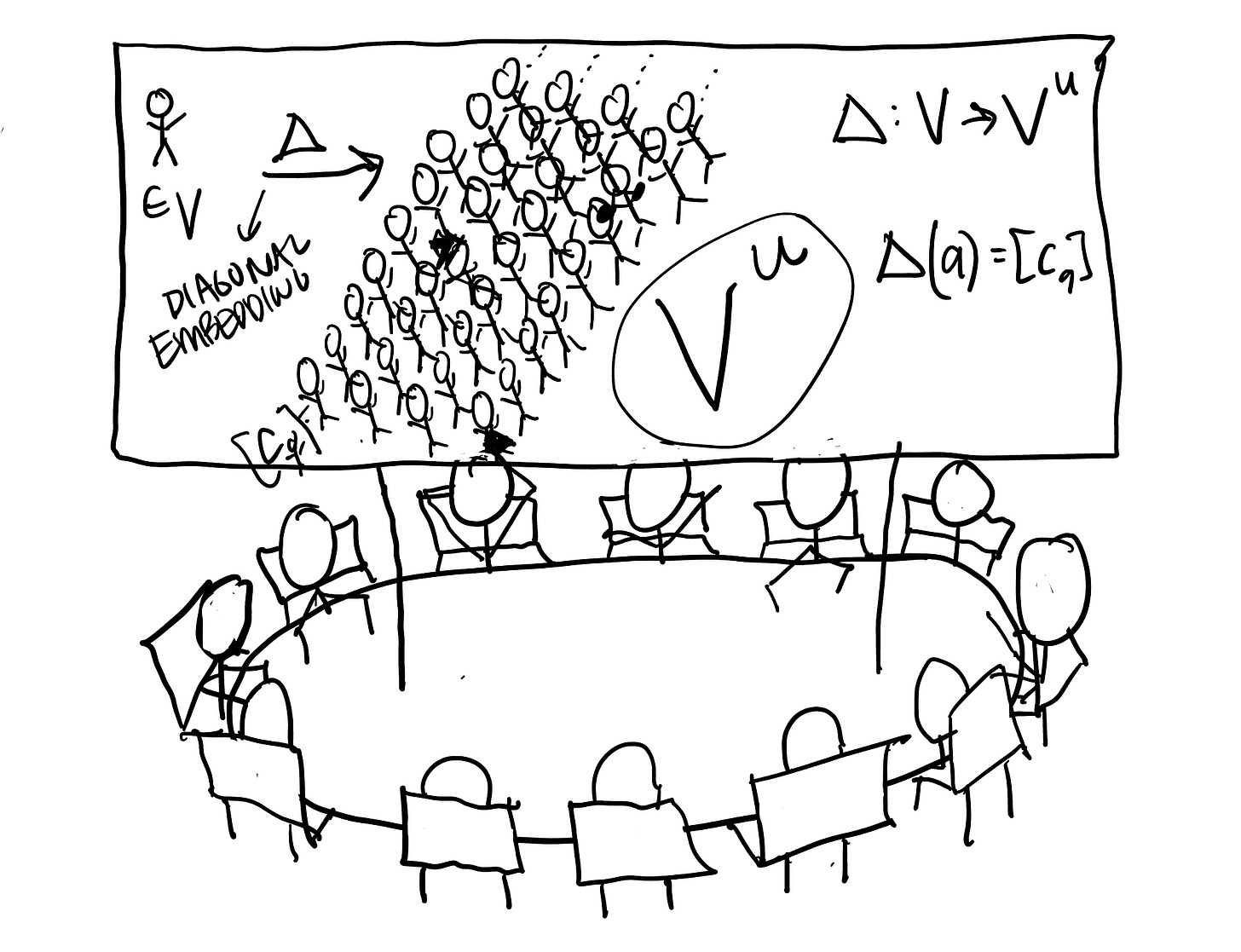
Producer 15: Yes, thank you. It’s called a diagonal embedding. Let me just show you on the image.

Producer 11: Oh I love embeddings!

Producer 100: This is going great guys! Good job!

Producer 29: Terrible!

Producer 30: This is a complete disaster!

Producer 28: There are many many functions that agree with any given f on a big set! Let

$f \in V^{\kappa}$

and let X be any set in the universe, then define a function

$f_{X}: \kappa \to V$

that is X on the first coordinate and then agrees with f on all the other coordinates. Wouldn’t you say that

$f_X \in [f]?$

Producer 30: I would indeed! And if X and Y are different sets then

$f_{X} \ne f_{Y}.$

$[f]$

is as big as the universe!

Producer 29: You can’t have a universe whose “elements” are classes!

Producer 3: You know what? I think we could also use a little coffee.

Producer 11: Wait a minute. I totally agree that there is a problem but wait this is so weird. Just this morning my friend Scott and I were having coffee. He tells me he had a dream about the ranks of sets and he came up with this cool way to turn a proper class into a set. We thought it was so funny but didn’t have a place to use it yet and we called it Scott’s trick.

Producer 15: Please. Save my idea!

Producer 11: Yeah it was really neat. We can all agree we have foundation and so we know that every set has a rank. Instead of thinking of the whole class, in this case

$[f]$

just consider the elements of this class which are of minimal rank. We could write

$[f]_{\mbox{set}} = \{ f \in [f] \ : \ \mbox{rk($f$) is minimal among the elements of $[f]$}\}$

and then

$[f]_{\mbox{set}}$

is a set and we can recover

$[f]$

from it so it seems to me that our ultrapower universe could be

$V^{U} = \{ [f]_{\mbox{set}} \ : \ f: \kappa \to V \}.$

I’m sure Scott would be happy to come fill in the details of how this works.

Producer 0: I know Scott he knows what’s up.

Producer 1: We should include the proof in the final script though.

Producer 0: Definitely. And I think it is fine if we even write

$[f]$

from now on when we really mean

$[f]_{\mbox{set}}$

since we all know what we are talking about.

Producer 15: That’s so great! We can continue!

Producer 23: Can we talk about the diagonal embedding now? Sounds amazing!

Producer 15: Let’s see I’ll bring up the image again here we go.

For every element a ∈ V let

$c_a : \kappa \to V$

to be the constant function with value a:

$(a, a, a, a, a, ....).$

Then

$[c_a]$

is in the ultrapower and is the set, thank you 11, of functions from κ to V that are the constant value a on a big set.

Then the diagonal embedding

$\Delta \ : \ V \to V^{U}$

maps any set in the universe to a set in the ultrapower

$\Delta(a) = [c_a].$

Producer 23: I love it so much! Is it an elementary embedding? Is that the whole idea?

Producer 67: Now what’s an elementary embedding again?

Producer 15: Would you like to show everyone 23?

Producer 23: It would be my absolute pleasure! Can everyone see?

An elementary embedding between two structures let’s say

$V \mbox{ and } V^U$

since that’s what we are talking about let’s say

$e: V \to V^U.$

Well this e is an elementary embedding if any formula

$\varphi$

with constants from V is true in V if and only if the formula

$\varphi$

with instead of its constants

$\langle a_n \rangle$

use constants

$\langle e(a_n) \rangle$

is true in

$V^U.$

It’s like you let the constants of the formula pass through the function and then the new formula with the new constants is still true in the new universe. In other words

$V \models \phi( \langle a_n \rangle ) \iff V^U \models \phi( \langle e(a_n)\rangle).$

Producer 15: Yes exactly 23 and here’s the amazing thing, as you predicted: the diagonal embedding is an elementary embedding! This is all on my friend Łoś he has this theorem and we can go through the whole proof right now if you want.

Producer 23: That is so amazing!

Producer 4: I have an idea. Instead of going through the whole proof let’s pick a good scene in V with actors and set from V, pass them through the diagonal embedding to get the ultrapower actors and set and then do the scene in the ultrapower and see if it is still good?

Producer 101: What a great idea! That sounds fun!

Producer 1: We’ll get Łoś to help us write the final script.

Producer 0: Great idea.

Producer 2: Aw can we do the scene at the end that one story? You know that one it just has two actors?

Producer 4: I know exactly what you are talking about from “The Forcing Federation League?”

Producer 2: Yess

Producer 4: Let’s first see the scene with actors from V that make it good.

After the celebration, Carmody and Indigo walked to their dorms.

Carmody: Thanks for believing so much in the mission of the league.

Indigo: Of course! I believe we will accomplish our mission. And most importantly I believe in you!

Carmody: I had a realization this past semester.

Indigo: About the forcing federation league?

Carmody: Well I did have a lot of realizations about the league but this was about something different.

Indigo: What did you realize?

Carmody: Well I thought that love was a metaphor but it turns out it’s a feeling.

Producer 2: Aw I love that scene! Looks good!

Producer 4: Let’s try to pass it through the diagonal embedding and watch in the ultrapower.

✌︎♐︎⧫︎♏︎❒︎ ⧫︎♒︎♏︎ ❍︎♏︎♏︎⧫︎♓︎■︎♑︎♋︎❒︎❍︎□︎♎︎⍓︎ ♋︎■︎♎︎ ■︎♎︎♓︎♑︎□︎ ⬥︎♋︎●︎🙵♏︎♎︎ ⧫︎□︎ ⧫︎♒︎♏︎♓︎❒︎ ♎︎□︎❒︎❍︎⬧︎

♋︎❒︎❍︎□︎♎︎⍓︎🖳︎ ❄︎♒︎♋︎■︎🙵⬧︎ ♐︎□︎❒︎ ♌︎♏︎●︎♓︎♏︎❖︎♓︎■︎♑︎ ⬧︎□︎ ❍︎◆︎♍︎♒︎ ♓︎■︎ ⧫︎♒︎♏︎ ❍︎♓︎⬧︎⬧︎♓︎□︎■︎ □︎♐︎ ⧫︎♒︎♏︎ ●︎♏︎♋︎♑︎◆︎♏︎

■︎♎︎♓︎♑︎□︎🖳︎ ⚐︎♐︎ ♍︎□︎◆︎❒︎⬧︎♏︎✏︎ ♌︎♏︎●︎♓︎♏︎❖︎♏︎ ⬥︎♏︎ ⬥︎♓︎●︎●︎ ♋︎♍︎♍︎□︎❍︎◻︎●︎♓︎⬧︎♒︎ □︎◆︎❒︎ ❍︎♓︎⬧︎⬧︎♓︎□︎■︎ ✌︎■︎♎︎ ❍︎□︎⬧︎⧫︎ ♓︎❍︎◻︎□︎❒︎⧫︎♋︎■︎⧫︎●︎⍓︎ ♌︎♏︎●︎♓︎♏︎❖︎♏︎ ♓︎■︎ ⍓︎□︎◆︎✏︎

♋︎❒︎❍︎□︎♎︎⍓︎🖳︎ ♒︎♋︎♎︎ ♋︎ ❒︎♏︎♋︎●︎♓︎⌘︎♋︎⧫︎♓︎□︎■︎ ⧫︎♒︎♓︎⬧︎ ◻︎♋︎⬧︎⧫︎ ⬧︎♏︎❍︎♏︎⬧︎⧫︎♏︎❒︎

■︎♎︎♓︎♑︎□︎🖳︎ ✌︎♌︎□︎◆︎⧫︎ ⧫︎♒︎♏︎ ♐︎□︎❒︎♍︎♓︎■︎♑︎ ♐︎♏︎♎︎♏︎❒︎♋︎⧫︎♓︎□︎■︎ ●︎♏︎♋︎♑︎◆︎♏︎✍︎

♋︎❒︎❍︎□︎♎︎⍓︎🖳︎ 🕈︎♏︎●︎●︎ ♎︎♓︎♎︎ ♒︎♋︎❖︎♏︎ ♋︎ ●︎□︎⧫︎ □︎♐︎ ❒︎♏︎♋︎●︎♓︎⌘︎♋︎⧫︎♓︎□︎■︎⬧︎ ♋︎♌︎□︎◆︎⧫︎ ⧫︎♒︎♏︎ ●︎♏︎♋︎♑︎◆︎♏︎ ♌︎◆︎⧫︎ ⧫︎♒︎♓︎⬧︎ ⬥︎♋︎⬧︎ ♋︎♌︎□︎◆︎⧫︎ ⬧︎□︎❍︎♏︎⧫︎♒︎♓︎■︎♑︎ ♎︎♓︎♐︎♐︎♏︎❒︎♏︎■︎⧫︎

■︎♎︎♓︎♑︎□︎🖳︎ 🕈︎♒︎♋︎⧫︎ ♎︎♓︎♎︎ ⍓︎□︎◆︎ ❒︎♏︎♋︎●︎♓︎⌘︎♏︎✍︎

♋︎❒︎❍︎□︎♎︎⍓︎🖳︎ 🕈︎♏︎●︎●︎ ⧫︎♒︎□︎◆︎♑︎♒︎⧫︎ ⧫︎♒︎♋︎⧫︎ ●︎□︎❖︎♏︎ ⬥︎♋︎⬧︎ ♋︎ ❍︎♏︎⧫︎♋︎◻︎♒︎□︎❒︎ ♌︎◆︎⧫︎ ♓︎⧫︎ ⧫︎◆︎❒︎■︎⬧︎ □︎◆︎⧫︎ ♓︎⧫︎❼︎⬧︎ ♋︎ ♐︎♏︎♏︎●︎♓︎■︎♑︎

Producer 2: You know I’m a very intuitive person and the scene feels good. It’s just

Producer 4: Kinda strange.

Producer 2: Unfamiliar.

Producer 15: Is my dream dead?

Producer 0: It’s not wrong it’s just weird.

Producer 1: Well it’s not transitive.

Producer ω: That’s ok! For the Löwenheim-Skolem downward flick we didn’t end up with a transitive model.

Producer ω₁: That’s true I can testify to that! We had

$\omega_1^M = \omega_1 $

so ω₁ was in M and it is really ω₁ but M is countable so it definitely can’t have all of the elements of ω₁.

Producer 0: There was no other way in that film. LS ↓ productions always end with a nontransitive universe.

Producer 16: Anybody into explosives?

Producer 15: What are you thinking?

Producer 16: The Mostowski Collapse.

Producer 17: Do we have the budget?

Producer 16: I think we can stretch it. I have some experience with this. We’d just need our ultrapower universe to be set-like, extensional, and well-founded. Can we get an ω₁-complete ultrafilter?

Producer 1: I can get us an ω₁-complete ultrafilter on κ. Consider it done.

Producer 15: Can you fill me in? I’ve never worked with a Mostowski Collapse.

Producer 16: The Mostowski Collapse will give us a transitive model M that is isomorphic to our ultrapower universe. Everything will look more familiar.

Producer 17: The isomorphism

$\pi: V^U \to M$

will map an element of our ultrapower to the set of its elements under the isomorphism

$\pi(a) = \{ \pi(b) \ : \ b \in_{U} a \}.$

Producer 18: In the end, we’ll get a transitive model M with

$(V^U, \in_U) \cong (M, \in).$

Producer 17: We can show that our ultrapower universe is set-like and extensional, but it might not be well-founded.

Producer 15: But our ultrapower universe is a model of ZFC so shouldn’t it believe in foundation?

Producer 18: It does believe in foundation and it does believe it is well-founded but some models of ZFC think that they are well founded but are not well-founded, like some ultrapowers.

Producer 16: But thanks to 1 who can get us an ω₁-complete ultrafilter on κ and thanks to this theorem we will be fine! The theorem says that if κ is a cardinal and U is an ultrafilter on κ then the following are equivalent:

$1) \ U \mbox{ is $\omega_1$-complete }$

$2) \ (V^U, \in_U) \mbox{ is well-founded.}$

and we probably don’t have time at this meeting but has everyone seen the equivalent definition using partitions? It says that U, a nonprincipal ultrafilter on κ, is μ-complete if and only if every partition of κ of less than μ many pieces has a piece in U. So helpful!

Producer 15: We saved it!

Producer 2: Let’s try the scene again.

After the celebration, Carmody and Indigo walked to their dorm rooms.

Carmody: Thank you for believing so much in the mission of the federation.

Indigo: Of course! I believe we will accomplish our mission. And most importantly I believe in you!

Carmody: I had a realization this past semester.

Indigo: About the forcing federation league?

Carmody: Well I did have a lot of realizations about the federation but this was about something else.

Indigo: What did you see?

Carmody: Well I always thought that love was a metaphor but it turns out it’s a feeling.

Producer 4: Looks great!

Producer 2: Swoon

Producer 15: So to make this film happen we make the ultrapower universe and then take the collapse.

Producer 23: We compose the embeddings to get an elementary embedding between the universe V and our new production M!

$j \ : \ V \to M$

$j(x) = \pi ( \Delta (x)).$

Producer 11: I can see it! Look how beautiful!

Producer 15: Wow.

Producer 111: You guys. I’m sitting here I’m sitting here and I’m just thinking. Is an ordinal in V still an ordinal in M? Is an ordinal in M an ordinal in V?

Producer 1: Since V and M are both transitive there is a lot of absoluteness between them.

Producer ω₁: Not everything is always absolute!

Producer 0: Totally true ω₁ but we do have the theorem that if

$M \subseteq N$

are productions with

$(M, \in) \models \mbox{ZFC} \mbox{ and } (N, \in) \models \mbox{ZFC}$

then the scene

$\varphi(x) := \mbox{"$x$ is an ordinal"}$

is absolute between M and N.

Producer 111: That’s just wonderful. Now I ask myself: if x is an ordinal is j(x) the same ordinal?

Producer 23: Now we’re getting down to it.

Producer 10: I think that if j maps every ordinal to itself then it is the identity map.

Producer 12: The ordinals are the backbone of the universe! Like us!

Producer 111: And my mind just won’t stop wondering. I’m wondering if j is not the identity then what is the first ordinal that is an ordinal on the other side but a different ordinal.

Producer 23: The critical point!

Producer 111: Yes that’s a good name for it. What is the critical point of j? And heck now I’m wondering what happens to κ under this embedding?

Producer 1: I’m listening and here’s what I propose to make this picture really capture the audience. Let me know what you think. We get a cardinal κ such that there is a nonprincipal ultrafilter U on κ that is κ-complete.

Producer 31: Won’t this stretch the budget? I just want to make sure we have enough room for costumes.

Producer 1: Here’s the thing. We already need an ω₁-complete ultrafilter, but if U is ω₁-complete it already μ-complete where μ is measurable. I say we make sure that measurable cardinal is κ itself.

Producer 0: Then the critical point of the embedding will be κ. And if κ is the critical point of any elementary embedding then it is measurable. It’s a new definition of measurable. We can put the details in the final script.

Producer 23: If κ is the first number moved by the embedding then j(κ) is mapped to an ordinal above κ since j is an increasing function. So there is nothing mapped to κ.

Producer 11: That means j is not onto since κ is not in the image of j. What if we thought of j[V], the image of V under j, as V. I mean they are isomorphic via j so in a way V is a subset of M.

Producer 15: This is my dream coming true. On the one hand

$ M \subseteq V$

because it’s V, it’s the universe. But on the other hand

$V \cong j[V] \subseteq M.$

What does everyone think? Is it a hit? Will people like it?

Producer 1: Definitely.

Producer 0: Well some people will like it.

Producer 15: Thank you everyone for your help! I think it is going to be a blockbuster!

Producer 30: No problem!

Producer 28: Glad to help!

Producer 29: My pleasure!

Producer 100: Great job guys!!

Producer 3: Everyone must be so ready for a snack and drink!?

Producer 5: Great idea I’ll help!

Thank you Osvaldo Guzmán González for helping me translate this ancient artifact, and for showing me all the details of all of the proofs! I would not want to do it without you!

Math and Art

Discussion about this post