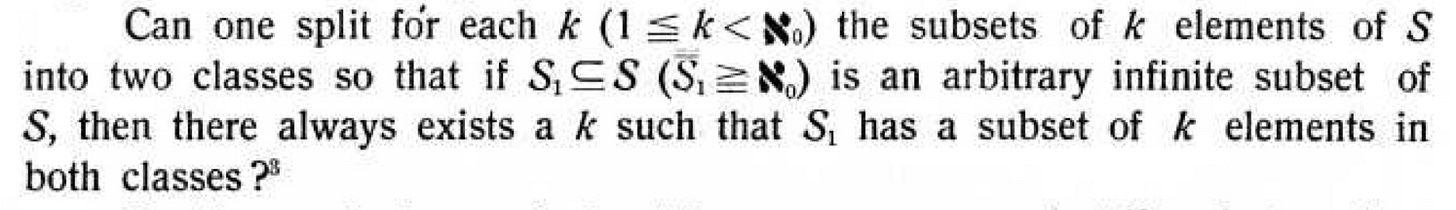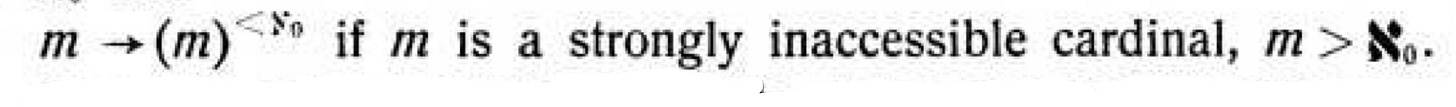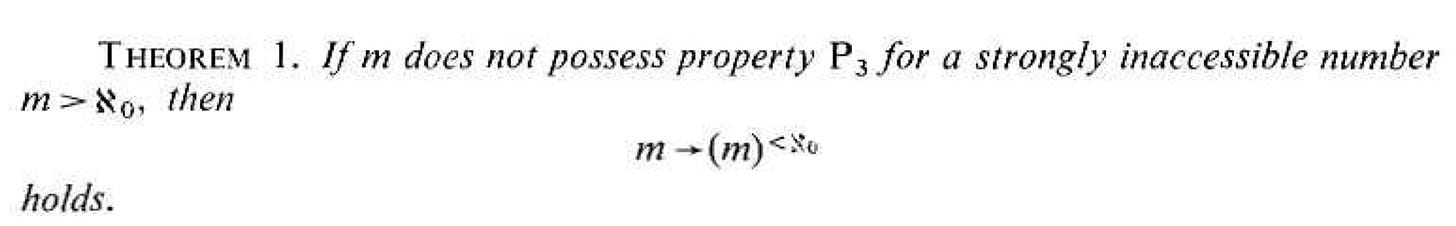In this chapter, we will see a top 10 list of large cardinals. We have met several large cardinals so far. We saw in chapter 3 that we cannot prove that large cardinals exist, nor can we prove that they are consistent relative to ZFC. Large cardinals notions are really axioms, and we can choose to believe in them. Of course, there are consequences of our beliefs. For example, if there is a measurable cardinal then V ≠ L (Scott’s theorem). This chapter will include the definitions of the large cardinals on the list, reflections on a papers written about the large cardinals, and further research. The criteria for the top 10 list are:
1) It is a large cardinal. For me κ is a large cardinal if it is worldly or more. That is, if
2) Simple to state the definition (sorry Woodin cardinals).
3) Not known to be inconsistent with ZFC (sorry Reinhardt cardinals).
4) Has an interesting paper about the large cardinal (I’m sure every large cardinal has this property).
These top 10 large cardinals would be considered wildly popular among set theorists, but there is probably a wide variety of opinions about large cardinals. The order of the list itself is somewhat arbitrary and somewhat intuitive.
For each large cardinal, there are 4 parts of the presentation. First, the definition of the large cardinal from Cantor’s attic (and perhaps Jech or Kanamori). Second, will be a reflection on the paper concerning the large cardinal, including the definition of the large cardinal in the paper. Third, will be the “philosophy” of the large cardinal - the word philosophy here is very loose - it will be an artistic impression of the bird that captures the essence of the bird and the bird’s own philosophy of the world based on its perspective. Fourth, will be ideas for further research that is connected to my own research and the theme of the book. The theme of the book which will come to fruition in the last chapter, chapter 7, is to demonstrate the almost one-to-one correspondence between the degrees of large cardinals and the forcings which gently destroy them.
They are grouped into parts, but I will post them one at a time.
CHAPTER 4: THE TOP 10 LARGE CARDINALS
PART 1: LARGE CARDINALS 10, 9, AND 8
PART 2: LARGE CARDINALS 7, 6, AND 5
PART 3: LARGE CARDINALS 4, 3, 2, AND 1
PART 4: THE LARGE CARDINAL CHAPTER PAINTING
PART 1: LARGE CARDINALS 10, 9, AND 8
Sunset by Felix Vallotton 1913
RAMSEY CARDINALS
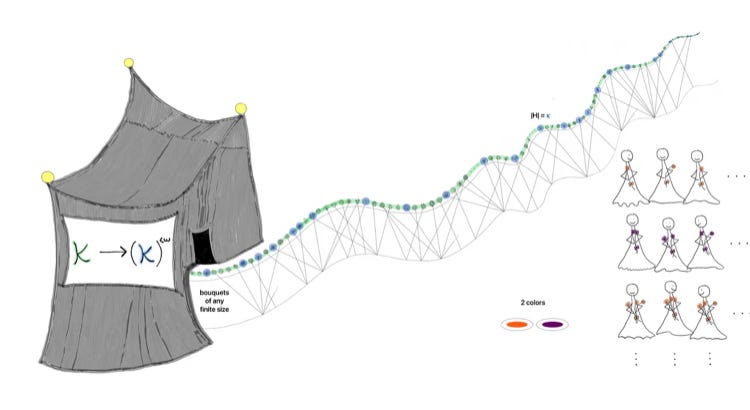
A cardinal κ is a Ramsey cardinal if it has the partition property
We’ll get back to Gitman’s many contributions to the study of Ramsey cardinals in a moment. First, let us go back to a paper written by Erdös and Hajnal in 1962:
SOME REMARKS CONCERNING OUR PAPER “ON THE STRUCTURE OF SET-MAPPINGS.” NON-EXISTENCE OF A TWO-VALUED σ-MEASURE FOR THE FIRST UNCOUNTABLE INACCESSIBLE CARDINAL
In this paper, they give the definition of a Ramsey cardinal along with the arrow notation.
The paper [5] is a 1956 paper by Erdös and Rado called “A partition calculus in set theory.” It is in this paper that the arrow notation is introduced, but the arrow notation for Ramsey cardinals is not included, nor does it seem to contain the idea of a Ramsey cardinal, but they wish to extend Ramsey’s theorem. They state Ramsey’s theorem from 1930 in “its simplest form.”
Let S be the set of all positive integers and suppose that all unordered pairs of distinct elements of S are distributed over two classes. Then there exits an infinite subset A of S such that all pairs of elements of A belong to the same class.
If we look back a little further to a paper published in 1952 by Erdös and Rado called “Combinatorial theorems on classifications of subsets of a given set” they also begin with Ramsey’s theorem and write about an unsolved problem for cardinals larger than the continuum.
Given an infinite set S, is it possible to divide all finite subsets of S into two classes in such a way that every infinite subset of S contains two finite subsets of the same number of elements but belonging to different classes?
I liked the notation in this paper for the set of all subsets of S which contain exactly n elements.
\(\Omega_n(S)\)
The 1962 paper by Erdös and Hajnal is about their paper from 1958
ON THE STRUCTURE OF SET MAPPINGS
which also includes the arrow notation and the idea of a Ramsey cardinal.
When I first started to read this paper, I thought perhaps there was a different definition of a strongly inaccessible cardinal because I saw this statement soon after the above question.
This would say that every inaccessible cardinal is a Ramsey cardinal, which is not true. And then there was this theorem from the companion paper “Some remarks concerning our paper…”
The property P₃ says that a cardinal is not measurable. So this theorem says that if m is measurable and m is inaccessible, then m is a Ramsey cardinal. At first, I thought the theorem was saying that if m is an inaccessible cardinal that is not measurable then it is Ramsey, which did not make sense. In my continued confusion, I asked a question on Mathoverflow, which was answered by Emil Jeřábek. I soon found out that Erdös and Hajnal had thought that strongly inaccessible cardinals were also measurable in the paper “On the structure of set mappings.” Once they realized that inaccessible cardinals are not necessarily measurable, they wrote “Some remarks on our paper…” where they showed that there are inaccessible cardinals that are not measurable. Also, since the Theorem 1 above is saying that if m is measurable and inaccessible then it is a Ramsey cardinal, it seems that they did not know that if a cardinal has the property of being a measurable cardinal then it is an inaccessible cardinal.
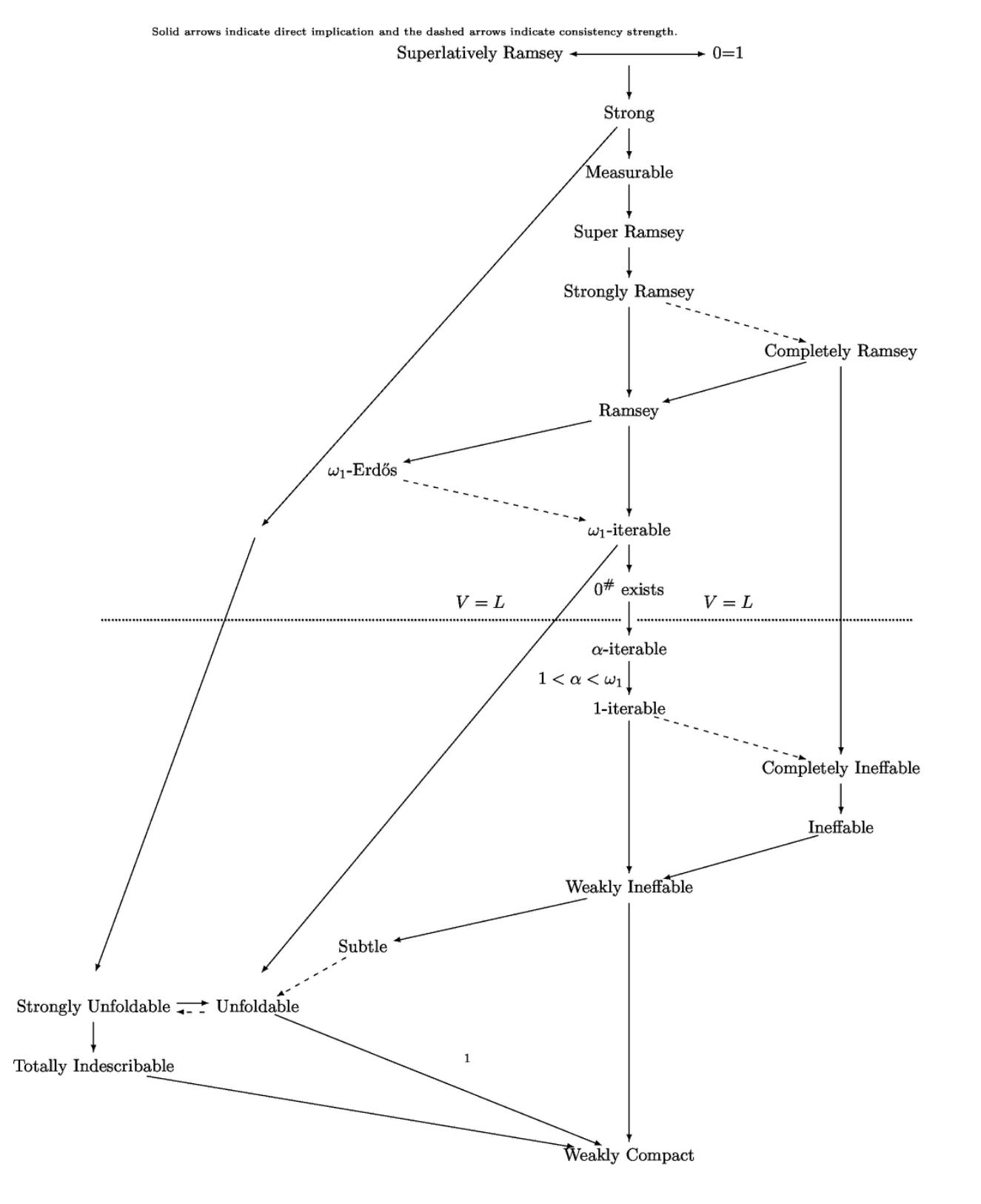
Since this time, there has been a lot of work done on developing definitions of large cardinals that extend the idea of a Ramsey cardinal. Here is a diagram created by Victoria Gitman that includes many of her “Ramsey-like” cardinals and how they fit into the large cardinal hierarchy.
Large cardinal chart of Ramsey-like cardinals by Victoria Gitman
The philosophy of Ramsey cardinals:
The bride sat upon her throne that she had made herself out of the frozen tears of potential bridesmaids. “It needs to be bigger! It needs to be better!” This bride wanted the most extravagant wedding possible. “How am I supposed to choose flowers and bridesmaids when everyone and everything is a fake and phony just to get into the wedding!?” That’s when the bride saw an ad for “Everlasting flowers.” The ad read, “at Everlasting flowers find your true bridesmaids and true flowers in your true colors…for a price.” The bride called immediately. “Make it happen!”
The bride was taken to a special garden where there were infinitely many flowers, each unique. The first set of infinitely many potential bridesmaids came into the garden, each chose one of the flowers and dipped it into one of the two color pools. A second set of infinitely many potential bridesmaids came into the garden, each chose a bouquet of two flowers and dipped the bouquet into one of the color pools. This continued at each finite step, that infinitely many potential bridesmaids came in and each chose a bouquet of that finite size.
Then with the wave of a wand, there appeared an infinite subset of the garden, as infinite as the garden itself, that sparkled. The bride saw that all of the bouquets of size 1 from this special part of the garden were all orange. She saw that all of the bouquets of size 2 from this special part of the garden were all maroon. She saw that all of the bouquets of size n from this special part of the garden were all the same color. She chose the bridesmaids that chose from the special sparking part of the garden as her bridal party, and the flowers in the special section as her flowers. “Victory is mine!”
FURTHER RESEARCH:
When I was in graduate school, I wondered if there were degrees of Ramsey cardinals (even though at the time I didn’t really know what a Ramsey cardinal was) because I knew it involved colors and my research involved degrees of large cardinals. I asked Victoria, and she thought about it for a while and then decided that there were, and then she talked to Miha Habič and together they defined the degrees of Ramsey cardinals and wrote a paper, A Mitchell-like order for Ramsey and Ramsey-like cardinals, that is now published in Fundamenta Mathematicae.
This paper is far too technical to be included here, but it fits perfectly with the eventual theme of the book about forcing to softly kill degrees of large cardinals. In the paper, they note that “Mitchell proved that Ramsey cardinals have an embedding characterization and Gitman used generalizations of it to define Ramsey-like cardinals…” They use these to embedding characterizations to define degrees of Ramsey cardinals. I would like to see the translation of these degrees into partition property definitions because the partition property version of Ramsey cardinals is the easiest to comprehend and visualize for me. Also, when I originally wondered about degrees of Ramsey cardinals, I was talking to Stevo Todorčević who has a strong interest in solving the infinite version of the Halpern–Läuchli theorem. For some reason, I thought if there were degrees of Ramsey cardinals, this might help solve this problem. It is unlikely but who knows?
